Math Teaching on Properties of Circles

<body><script type="text/javascript"> function setAttributeOnload(object, attribute, val) { if(window.addEventListener) { window.addEventListener('load', function(){ object[attribute] = val; }, false); } else { window.attachEvent('onload', function(){ object[attribute] = val; }); } } </script> <div id="navbar-iframe-container"></div> <script type="text/javascript" src="https://apis.google.com/js/platform.js"></script> <script type="text/javascript"> gapi.load("gapi.iframes:gapi.iframes.style.bubble", function() { if (gapi.iframes && gapi.iframes.getContext) { gapi.iframes.getContext().openChild({ url: 'https://www.blogger.com/navbar.g?targetBlogID\x3d501995071564654298\x26blogName\x3dProperties+of+Circles\x26publishMode\x3dPUBLISH_MODE_BLOGSPOT\x26navbarType\x3dBLUE\x26layoutType\x3dCLASSIC\x26searchRoot\x3dhttps://mathteachingonpropertiesofcircles.blogspot.com/search\x26blogLocale\x3den_US\x26v\x3d2\x26homepageUrl\x3dhttp://mathteachingonpropertiesofcircles.blogspot.com/\x26vt\x3d-253807637775335736', where: document.getElementById("navbar-iframe-container"), id: "navbar-iframe", messageHandlersFilter: gapi.iframes.CROSS_ORIGIN_IFRAMES_FILTER, messageHandlers: { 'blogger-ping': function() {} } }); } }); </script>

Properties of Circles

*Welcome to the Math Teaching Blog*

*Please Click the Words to Navigate*

Tuesday, July 21, 2009

Teaching Concept Eleven

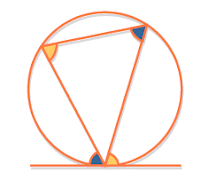
Let us look at the last Property of the Circle:
- The alternate segment theorem states that an angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.

- How to proof if the angle between a tangent and a chord through the point of contact is always equal to the angle in the alternate segment.
Proof:
- angle SPT= 90° (right angle in a semicircle)
- angle x+ angle y = 90° (angle sum of triangle)
- angle y+ angle z= 90° (tangent perpendicular to radius)
- angle x= angle z
- angle PTB= angle PST
- angle PST= angle PQT ( angles in same segment)
- angle PTB= angle PQT

- Let us try some simple questions:

- In the figure shown, line PA and line PB are tangents to the circle. angle ABP= 60° and BAC= 40°. Find the value of angle x and angle y.

- Calculate the value of angle x and angle y.

# posted by Properties of Circles at 6:32:00 AM